Benchmarking Edge Regression on Temporal Networks

Posted by Muberra Ozmen, Florence Regol, and Thomas Markovich on 

At Cash App, one of our aims is to understand our customers through the transactions between them, allowing us to personalize their experience and meet their needs more effectively. Our peer-to-peer transaction data is inherently graph-structured, where customers are represented as nodes and transactions as edges. With millions of transactions processed monthly on average, this graph is constantly evolving. This raises a crucial question: “How can we best leverage this data to extract the most valuable insights?”

img

The current literature offers a straightforward solution: train a Temporal Graph Neural Network (GNN) to perform link prediction, such as predicting “Will Cat send money to Fox next week?”, and then use the learned embeddings for various downstream tasks. However, temporal link prediction overlooks a key piece of information — edge features — e.g. “transaction amount” which are especially valuable in the context of a transaction network.

Motivated by this gap in the literature, we define a new frontier Temporal Edge Regression (TER) as a distinct task in temporal graph learning, focusing on predicting continuous target values for edges in dynamic networks. In this post, we’ll provide an overview of our latest research, Benchmarking Edge Regression on Temporal Networks, published in the Journal of Data-centric Machine Learning Research.

Here’s a quick overview of our contributions:

Formalizing Temporal Edge Regression

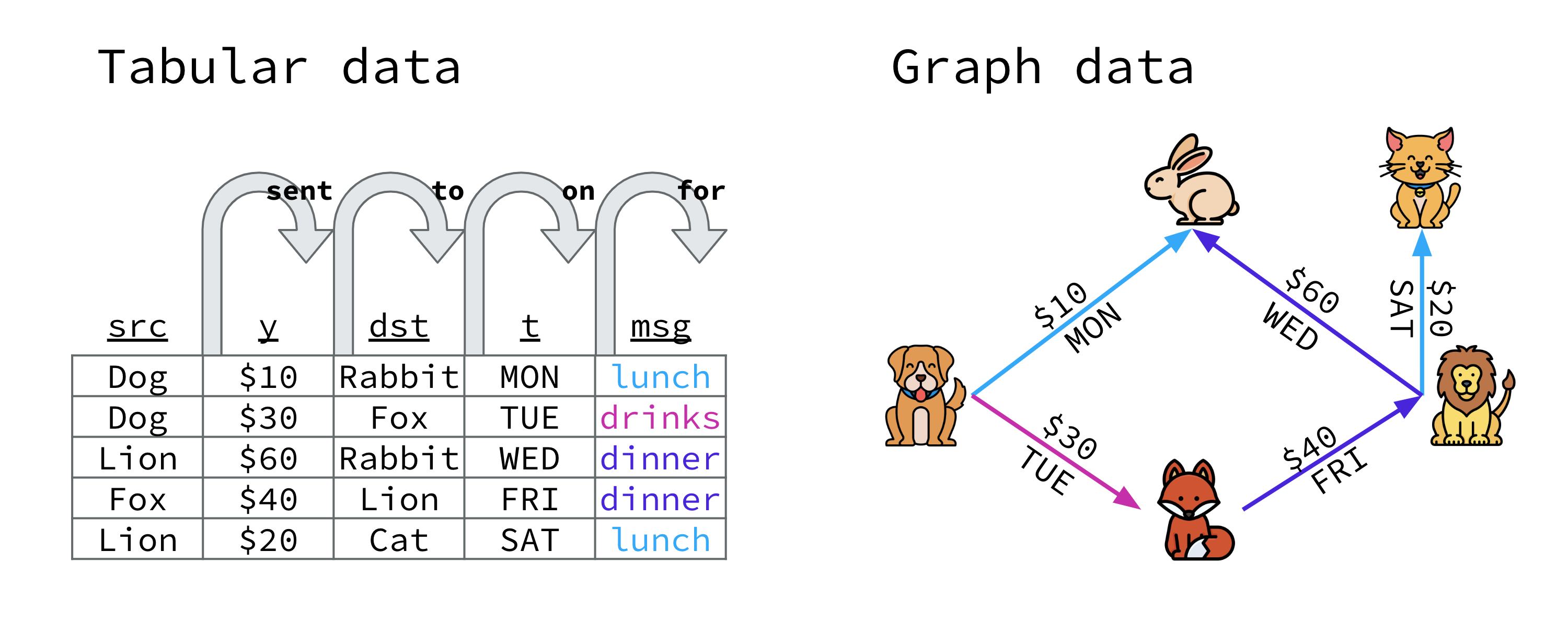
We consider a dynamic graph setting in which the set of vertices is fixed, and the edges appear over time. An edge, $e_j$, is composed of 4 components; the index of the source vertex $s_j$, the index of the destination vertex $d_j$, a feature vector of the edge $\mathbf{z}_j$, and the target value of interest $y_j$. Each of these components can be observed at different times;

We strictly assume that ${tx}_j \leq {tz}_j \leq {ty}_j$. That is, ${tx}_j$ marks the announcement time of interaction $j$ and ${ty}_j$ marks the completion time of the interaction. At any time $t$, we can therefore define a set of completed interactions $\mathcal{E}^{\operatorname{C}}(t) = {j: {ty}_j \leq t}$ and a set of announced but incomplete interactions $\mathcal{E}^{\operatorname{A}}(t) = {j: {tx}_j \leq t, {ty}_j > t }$.

img

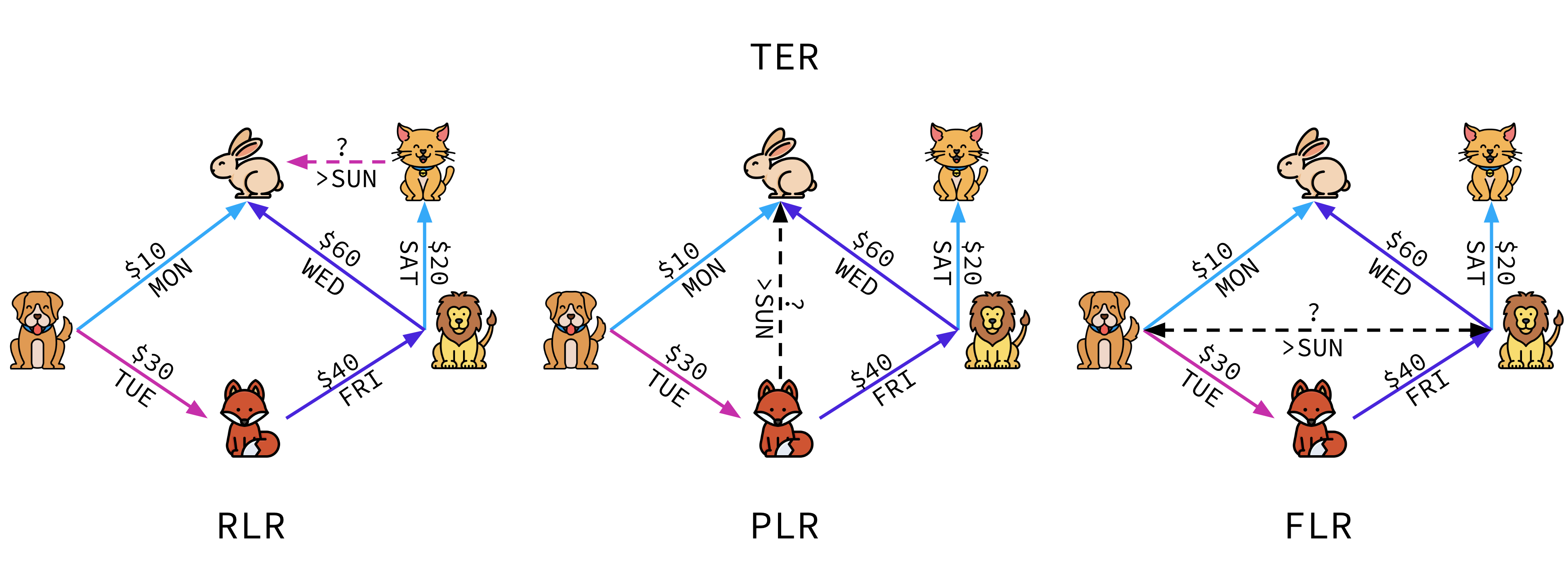
In TER, the goal is to build a classifier that maps the known components of announced interactions to their target values. This prediction is informed by the set of completed interactions at any given time $t$. We further define variations of the problem based on the relationships between observations that compose an event:

is known about the future interactions at the inference time.

Benchmark Datasets

One of the key challenges we face in TER is the lack of datasets that are designed for edge-focused learning. To address this, we’ve introduced four novel datasets that capture the dynamics needed for edge regression tasks:

These datasets provide a foundation for researchers to explore edge-based predictions in dynamic networks, helping advance the state of temporal graph learning. The applications of TER extend far beyond academic research. Whether it’s predicting delays in transportation systems, anticipating financial risks, or analyzing social interactions, TER has broad potential across many industries.

Model Comparison

img

We evaluated various models on these datasets,

While GNN-based methods generally outperform simpler baselines, our results show that no existing architecture fully addresses the unique challenges of TER. The architecture of current models is largely designed for node-based tasks, which leaves room for innovation in edge regression. This highlights the need for new, tailored approaches for TER.

Conclusion

The introduction of Temporal Edge Regression as a benchmark task, along with our newly proposed datasets, marks a significant milestone in the field of temporal graph learning. By focusing on the dynamics of relationships between entities, TER opens up new avenues for research and practical applications. As we continue to refine our models and datasets, we believe TER will play a critical role in advancing machine learning for complex, evolving systems.

Explore our paper if you are interested in more details and stay tuned for more updates as we explore the fascinating possibilities of temporal edge regression and its impact on real-world challenges.

References

[1] Souza Gomes, S. (2022). Dataset Epic Games. https://doi.org/10.5281/zenodo.7606569.

[2] Trivedi, P. (2021). Flight delay and causes dataset. https://www.kaggle.com/datasets/undersc0re/flight-delay-and-causes..

[3] Department of Transportation. (2017). 2015 Flight Delays and Cancellations. https://www.kaggle.com/datasets/usdot/flight-delays.

[4] La Cava, L., Costa, D., & Tagarelli, A. (2023). Sonar: Web-based tool for multimodal exploration of non-fungible token inspiration networks. In Proceedings of the 46th International ACM SIGIR Conference on Research and Development in Information Retrieval.

[5] Costa, D., La Cava, L., & Tagarelli, A. (2023). Show me your NFT and I tell you how it will perform: Multimodal representation learning for NFT selling price prediction. In Proceedings of the ACM Web Conference 2023.

[6] Kipf, T. N., & Welling, M. (2017). Semi-supervised classification with graph convolutional networks. In Proceedings of the International Conference on Learning Representations (ICLR). https://openreview.net/forum?id=SJU4ayYgl.

[7] Hamilton, W., Ying, Z., & Leskovec, J. (2017). Inductive representation learning on large graphs. In Advances in Neural Information Processing Systems (NeurIPS). https://proceedings.neurips.cc/paper/2017/file/5dd9db5e033da9c6fb5ba83c7a7ebea9-Paper.pdf

[8] Velickovic, P., Cucurull, G., Casanova, A., Romero, A., Lio, P., & Bengio, Y. (2018). Graph attention networks. In Proceedings of the International Conference on Learning Representations (ICLR). https://openreview.net/forum?id=rJXMpikCZ.

[9] Yun, S., Jeong, M., Kim, R., Kang, J., & Kim, H. J. (2019). Graph transformer networks. In Advances in Neural Information Processing Systems (NeurIPS). https://proceedings.neurips.cc/paper/2019/file/9d63484abb477c97640154d40595a3bb-Paper.pdf.

[10] Rossi, E., Chamberlain, B., Frasca, F., Eynard, D., Monti, F., & Bronstein, M. (2020). Temporal graph networks for deep learning on dynamic graphs. In ICLR 2020 Workshop on Graph Representation Learning. https://arxiv.org/abs/2006.10637.